고1 무리함수 격자점 답 5번입니다 부탁해요

답 29개
영역의 경계 및 교점 확인:
주어진 영역은 y축(x=0)과 두 곡선으로 둘러싸여 있습니다.
두 곡선의 교점을 찾기 위해 방정식을 연립합니다:
24/(x−12)+8=√x
. 이 방정식의 해를 구하면 대략적인 교점의 x좌표를 알 수 있지만,
정수점 계산에는 필요하지 않을 수 있습니다.
x=0 일 때, 첫 번째 곡선은 y=24/-12+8=-2+8=6을 지나고,
두 번째 곡선은 y=0 을 지납니다.
영역은 0≤x≤x교점 x≤y≤24/(x−12)+8 로 정의됩니다.
하지만 x가 0에서 12 사이일 때 분모가 음수이므로, 유리함수의 그래프는 감소하며
y값이 √x 보다 크지 않습니다.
문제의 의도는 아마도 x>0영역에서 두 곡선이 만나는 지점까지의 영역을 의미하는 것으로 보입니다.
x=9일 때 두 함수 값이 y=√9=3과 y=24/(9−12) +8=24/(-3) +8=-8+8=0으로 같지 않으므로,
교점은 x=9 보다 큰 값에서 형성됩니다.
정수 x좌표별 정수 y좌표 계산:
두 곡선과 y축으로 둘러싸인 영역은 실제로는 x가 증가함에 따라 두 곡선 사이의 간격이 넓어지다가 교점에서 닫히는 형태가 아닐 수 있습니다.
문제의 답이 29개라는 점을 고려하여, x가 특정 범위 내의 정수일 때, 각 x 에 대해 가능한 정수
y의 개수를 직접 계산합니다.
x가 0일 때: y는 0부터 6까지 (7개: 0, 1, 2, 3, 4, 5, 6)
x가 1일 때: y는 √1 =1 부터 24/(1−12)+8=24/(-11)+8≈5.8까지 (5개: 1, 2, 3, 4, 5)
x가 2일 때: y는 √2 ≈1.4 부터 24/(2−12) +8=24/(-10) +8=5.6 까지 (4개: 2, 3, 4, 5)
x가 3일 때: y는 √3 ≈1.7부터 24/(3−12)+8=24/(-9)+8≈5.6까지 (4개: 2, 3, 4, 5)
x가 4일 때: y는 √4 =2 부터 24/(4−12)+8=24/(-8)+8=5까지 (4개: 2, 3, 4, 5)
x가 5일 때: y는 √5 ≈2.2부터 24/(5-12)+8=24-7+8≈4.6까지 (2개: 3, 4)
x가 6일 때: y 는 √6≈2.4 부터 24/(6−12)+8=24/(-6)+8=4까지 (2개: 3, 4)
x가 7일 때: y는 √7≈2.6부터 24/(7−12)+8=24/(-5)+8=3.2까지 (1개: 3 )
x가8일 때 : y 는 √8≈2.8부터 24/(8−12)+8=24/(-4)+8=2까지 (0개: 해당 없음)
x=8 이후로는 유리함수 값이 x값보다 작아지므로 영역이 닫힌 것으로 볼 수 있습니다.
총 개수 합산:x값에 따른 정수 y좌표의 개수를 모두 더하면 다음과 같습니다.
7+5+4+4+4+2+2+1+0=29
괴산선비의 화학, 수학 이야기 : 네이버 블로그
 괴산선비의 화학, 수학 이야기 : 네이버 블로그
괴산선비의 화학, 수학 이야기 : 네이버 블로그 수학, 화공, 화학 마스터 네이버 파워지식IN
blog.naver.com
-
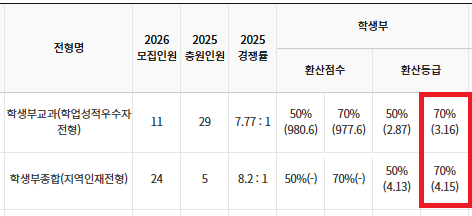
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -

아이폰 16, 16프로 케이스 호환 가능한가요? 16을 쓰고 있는데 일반형은 케이스가 많이 없고 프로형은 많아서
2025.12.01 -

임영웅 11월 브랜드평판 순위 알고싶어요 임영웅 11월 브랜드평판에서 스타부문에서의 임영웅 순위 알고싶어요
2025.11.30 -

전주 고등학교 다자녀 제가 2027학년도 고등학교 입학생인데요 지망하는 학교가 전주 한일고인데 1. 다자녀
2025.11.30 -
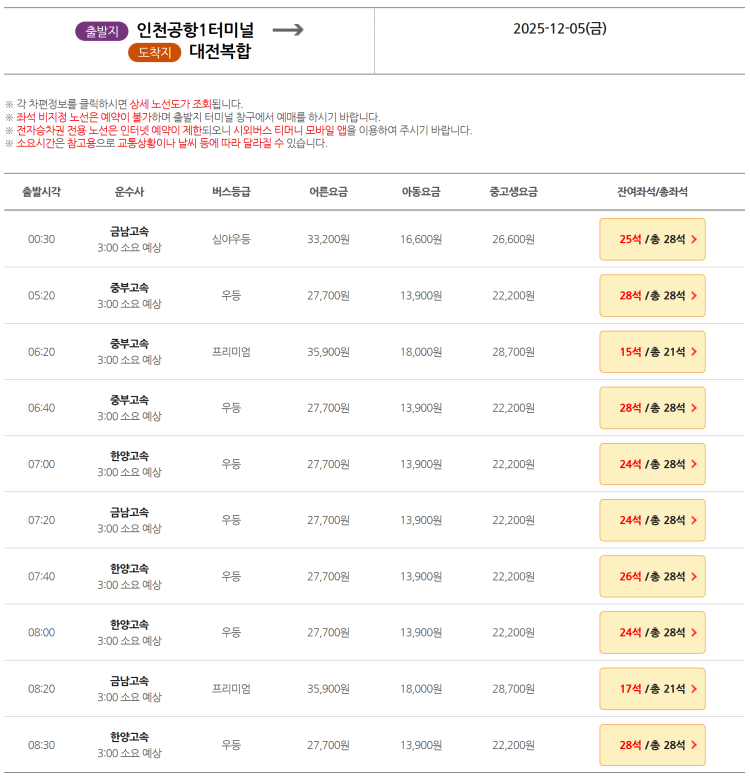
고속버스 예매 인천공항에서 대전으로 가는 버스를 이용하려하는데 버스 노선이 인천공항 2터미널에서 출발해
2025.11.30 -

어떤 야구선수 싸인일까요? 제가 옛날에 롯데 자이언츠 선수한테 싸인받은 싸인볼을 오늘 찾았네요. 어떤
2025.11.29
